
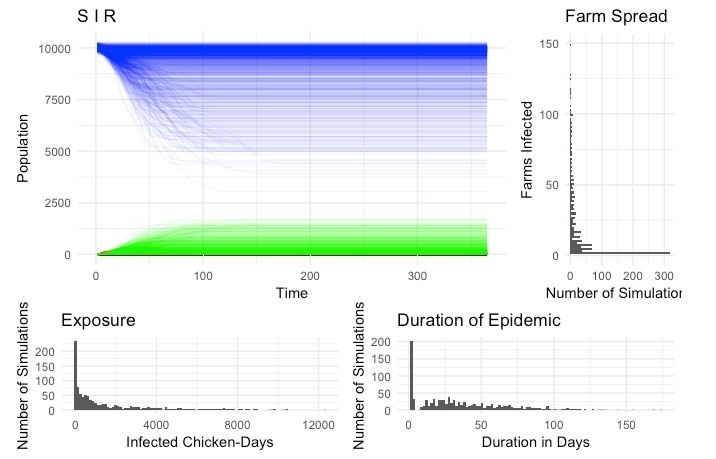
African Sustainable Livestock 2050
Aishwarya Venkat
EcoHealth Net Research Exchange Intern, Summer 2017





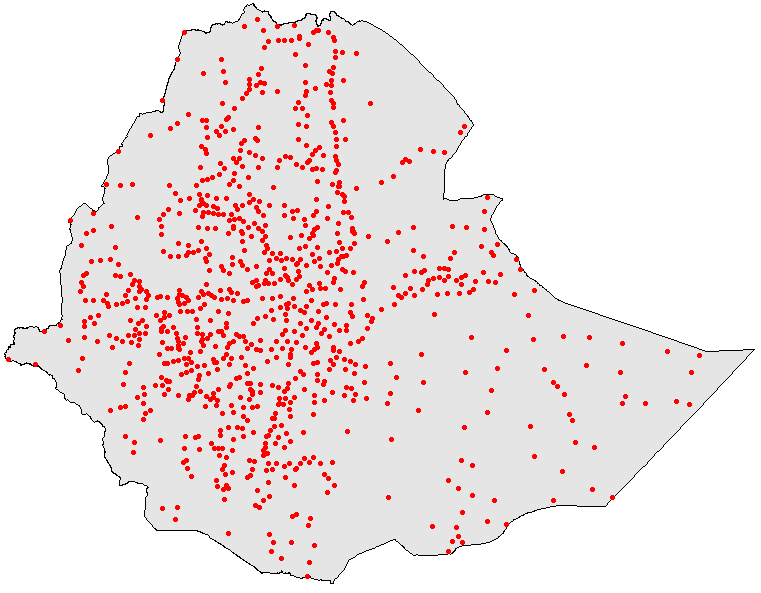
Households
Commercial Farms
Markets

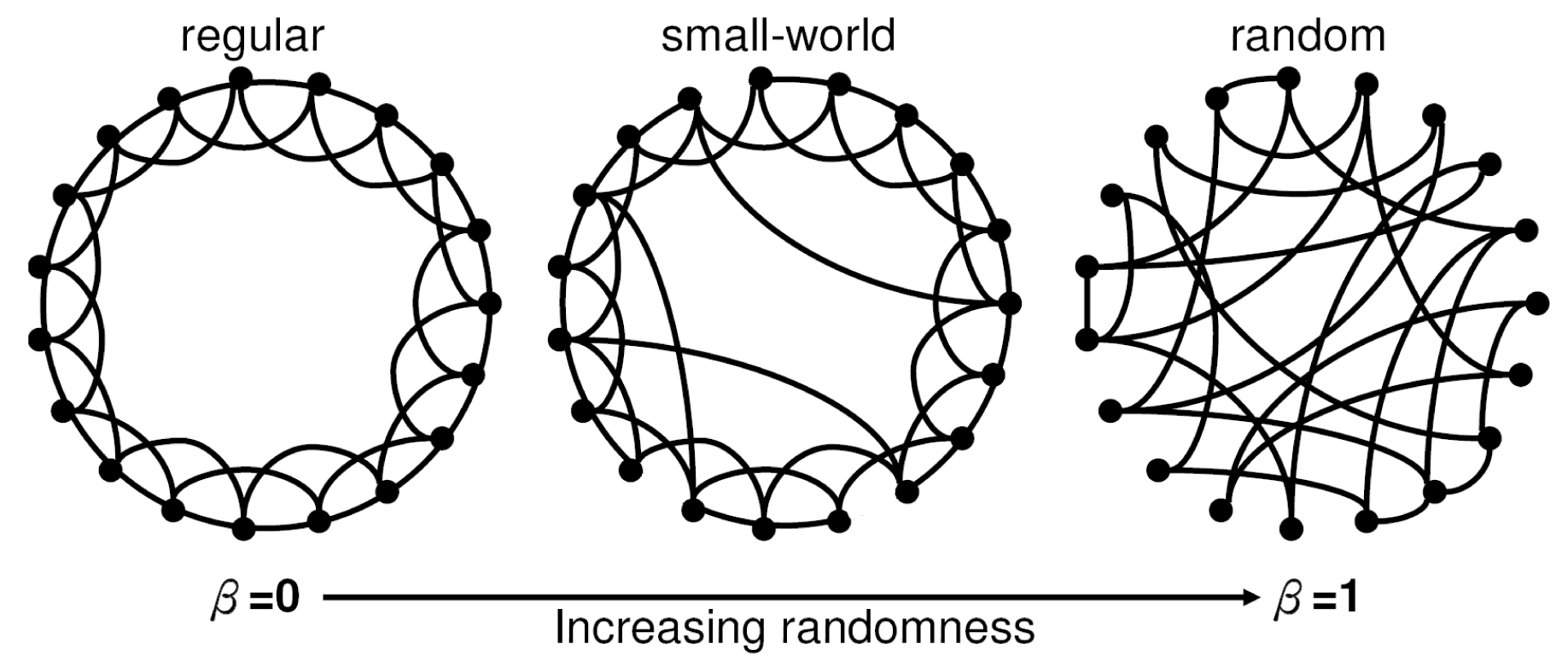
Watts, Duncan J., and Steven H. Strogatz. Collective dynamics of 'small-world' networks, Nature 393.6684 (1998): 440
## HHID EAID Latitude Longitude Household.Weight Chickens
## 1 87095 1912049 9.324 38.592 3971 8
## 2 86375 1270896 10.394 38.225 4752 2
## 3 84926 1391416 15.392 39.212 3230 4
Surveys provide approximate location information
Representative households are actually spread out across survey enumeration areas
Get number and sizes of commercial farms from literature, poultry sector reports (Ethiopia, Kenya, Uganda), or scraped from OIE & FAO EMPRES-I outbreak data
Fit lognormal model to farm size, sample randomly from distribution until value adds up to total estimated intensive chicken population

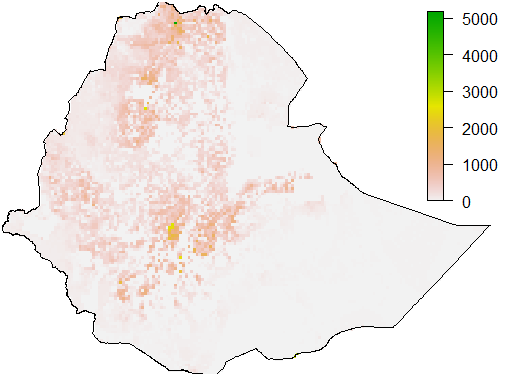
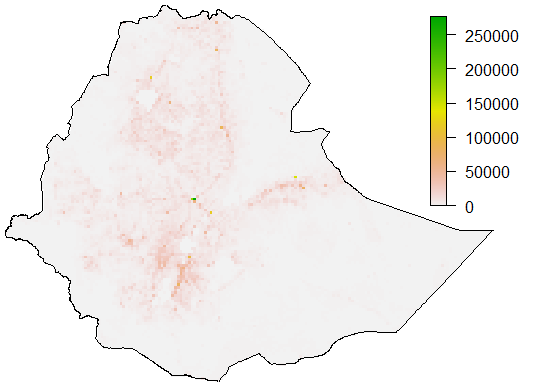
Ethiopia, Uganda, Kenya: Intergovernmental Authority on Development (IGAD)
Burkina Faso, Egypt, Nigeria: Populated Places data from OpenStreetMap and SEDAC GRUMP

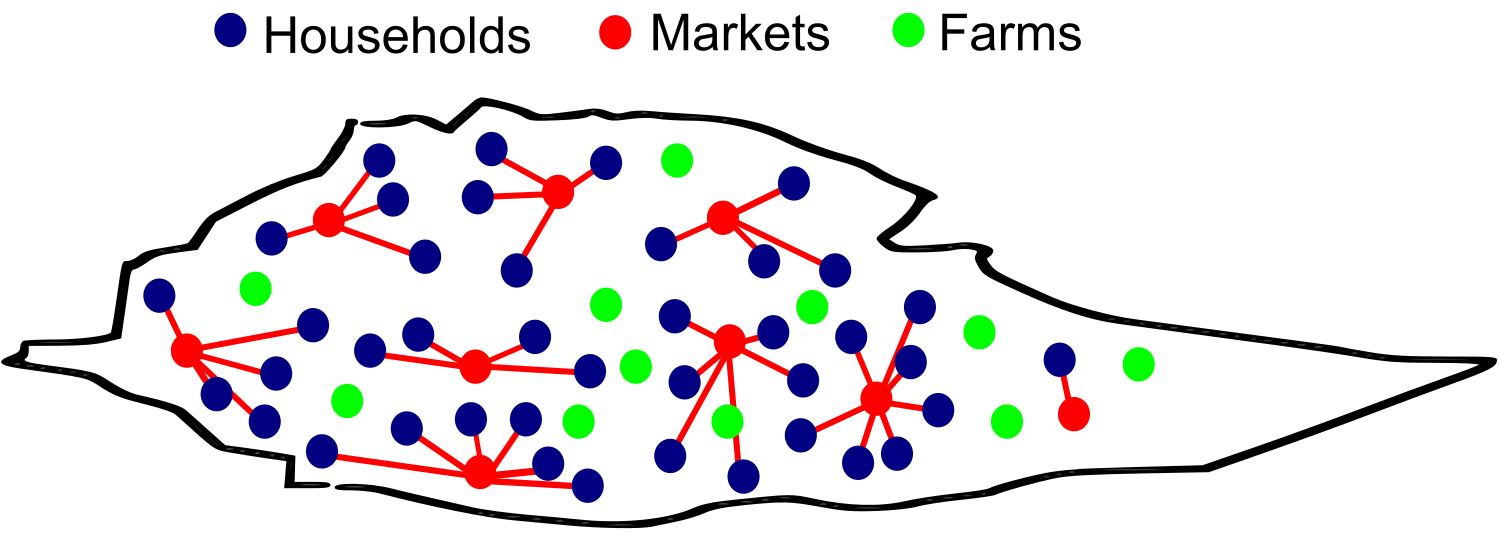
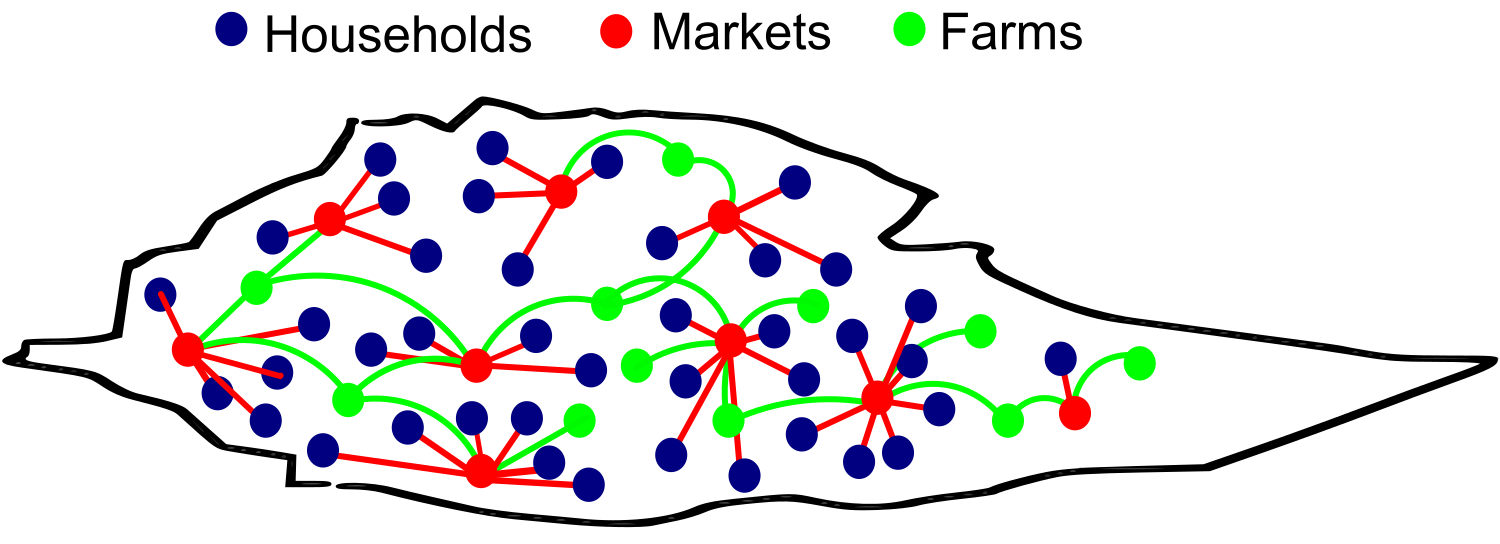
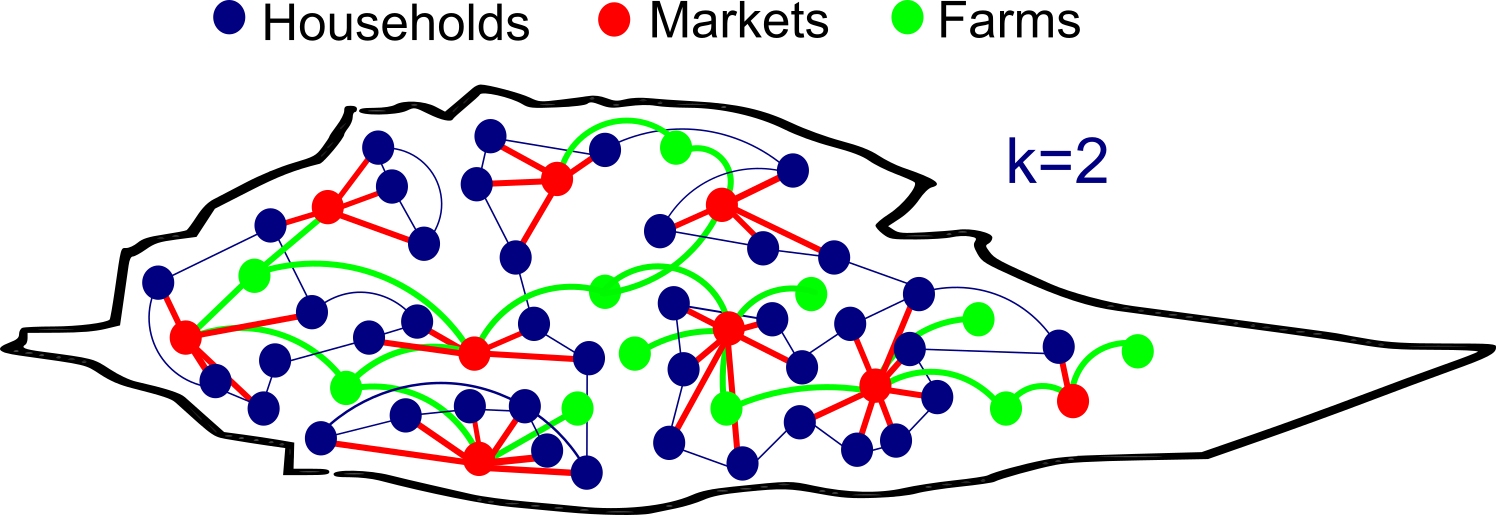
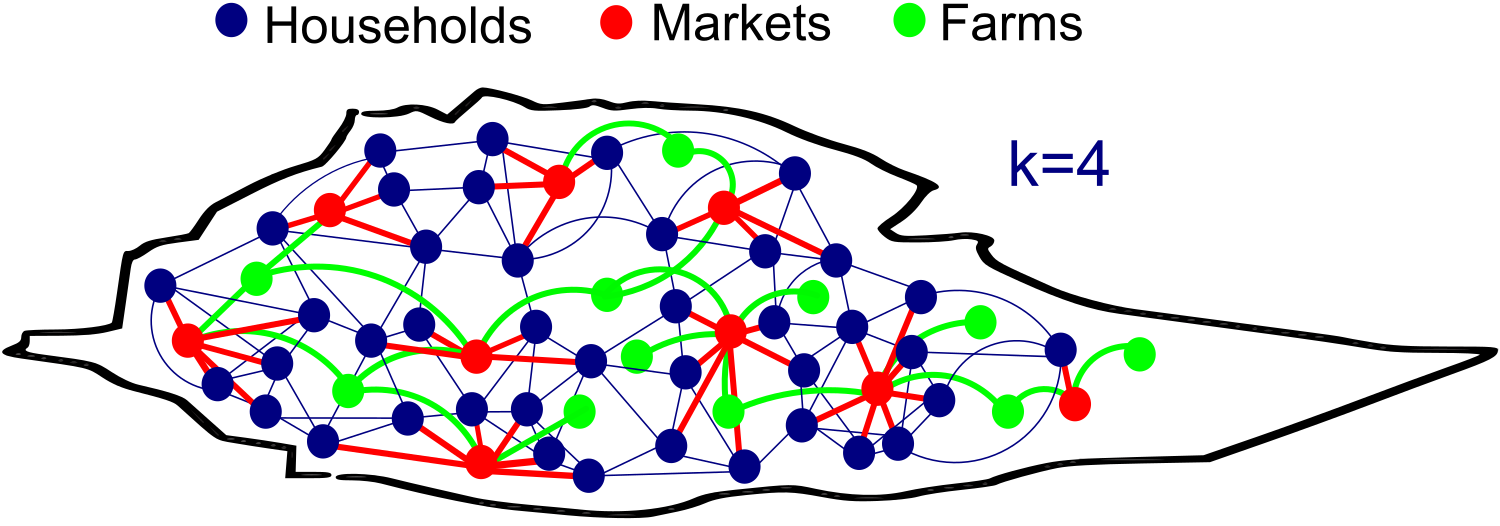
\[p_{u,v} = min\Bigg(\kappa_u\kappa_v\frac{f(d_{uv})}{\rho\langle\kappa\rangle},1\Bigg)\]
$u,v = $ two nodes (any of households, markets, farms)
$ p = $ probability of connection between nodes \(u\) and \(v\)
$f(d_{uv}) = $ exponential decay kernel connecting nodes, defined by a distance (rate) at which 50% of nodes in country are connected
$\kappa = $ expected degree of connections per node (Poisson distributed across nodes)
$\langle\kappa\rangle = $ average degree of connections for all nodes
$\rho = $ density of nodes within country
Lang, John, et al. Random Spatial Networks: Small Worlds without Clustering, Traveling Waves, and Hop-and-Spread Disease Dynamics. arXiv:1702.01252 (2017).
Noam Ross
Cale Basaraba
Allison White
Carlos Zambrana-Torrelio
Modeling & Analytics team

Orsolya Mikecz
Antonio Mele
Ugo Pica-Ciamarra

/
#